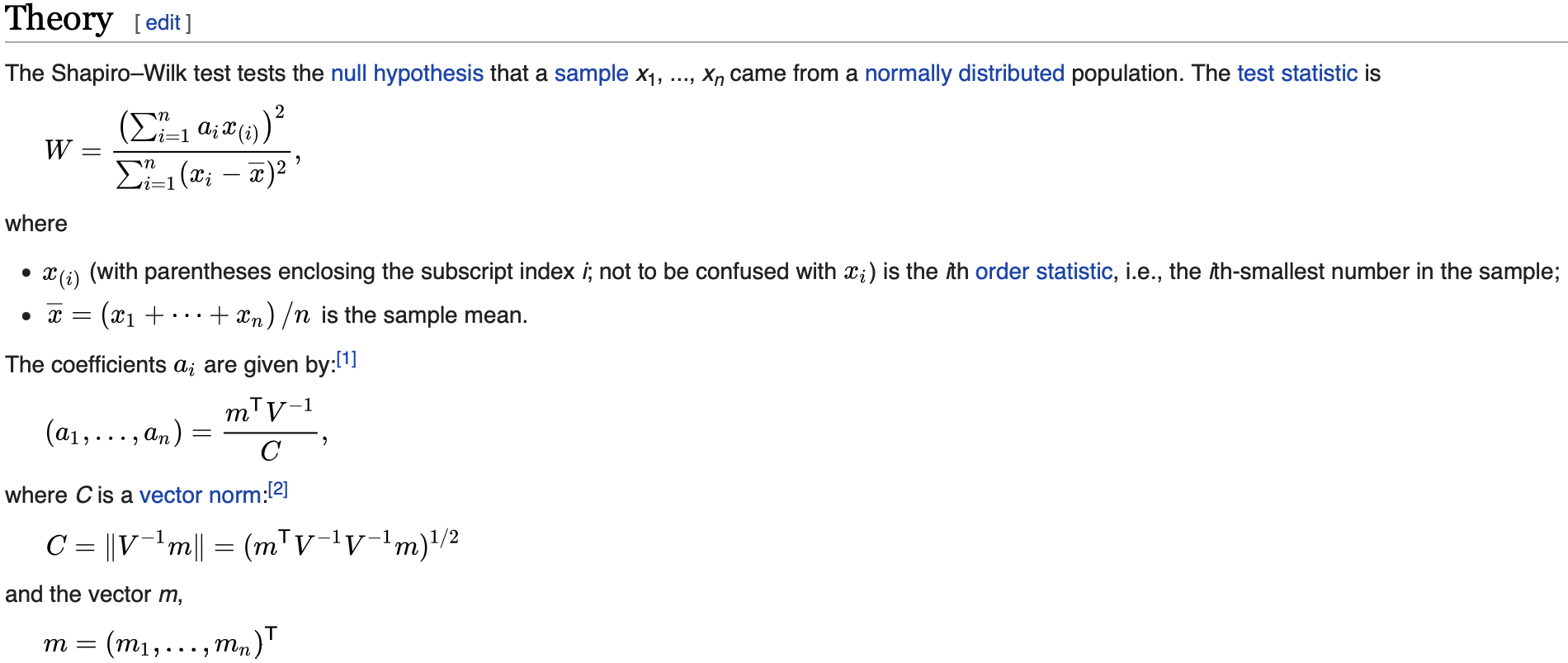
검정통계량 W의 원리는 선형모형에서 최소제곱법을 이용하여
근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합(SS)이 최소가 되는 해를 구하는 방법입니다
이 방법은 값을 정확하게 측정할 수 없는 경우에 유용하게 사용될 수 있으며, 특히 그 계의 방정식이 어떤 형태인지를 알고 있을 때 방정식의 상수 값들을 추정하는 데에 사용되는데 즉 여기에서는 모수값들을 찾는데 이용되어집니다
$$ E(x)_{i}^{}=m_{i}^{} $$ $$ m=(m_{1}^{},....m_{n}^{})^T $$
여기서 벡터 m은 표준 정규 분포에서 샘플링된 독립적이고 동일하게 분포된 확률 변수의 기대값 으로 구성됩니다.
$$ cov(x_{i}^{},x_{j}^{})=v_{ij}^{} $$ $$ V=(v_{ij}^{}) $$
여기서 V는 공분산 행렬 입니다
$$ y_{i}^{}=(y_{1}^{},...y_{n}^{})^T $$
y' = (y,, ...,y,) 순서가 지정된 임의 관측값의 벡터를 나타냅니다.
목표는 평균 과 분산 을 알 수 없는 정규 분포의 표본이라는 가설에 대한 검정을 도출하는 것입니다.
분명히, {y,}가 정규분포 이면 yi는 다음과 같이 표현될 수 있습니다.
$$ _{}^{}y_{i}=\mu +\sigma x_{i}^{} $$
일반화된 최소 자승 정리(Aitken, 1938; Lloyd, 1952)에서 평균 과 표준편차 의 가장 좋은 선형 비편향 추정값은 2차 형식 $$ (y-\mu 1-\sigma x_{i}^{})^TV_{}^{-1}(y-\mu 1-\sigma m) $$ 으로 표현될수있으며 여기서 1' = (1,1,...,1) 행백터로 표현됩니다.
Shapiro wilk test의 기본 검정은
H0:표본이 정규분포를 따른다
H1:표본이 정규분포를 따르지 않는다
따라 p-value가 0.05 이상이면 대립가설을 기각 즉 정규분포를 따른다 라는 기본검정원리입니다
검정통계량 W
$$ W=\frac{\left\{\sum_{i=1}^{n}a_{i}X_{(i)} \right\}^2}{\sum_{i=1}^{n}\left (X _{i}-\bar{X} \right )^2} $$